It’s The New World Order – Quantum Computers Are On Course To Rule Our Future
Posted By thestatedtruth.com on July 23, 2017
Once governments perfect Quantum, there will be a new world order and Bitcoin and other cryptocurrencies may be the first easy target. This means many things thought to be secret – won’t be secure in the not to distant future. Quantum is in early stages of development, but it already can break 32 characters long passwords in just a few minutes, far faster than conventional computing power. Perfect Quantum, and things will never be the same. The race is on.
What is Quantum Physics?
Quantum Physics basically allows for particles to be in two states at the same time one is the wave state and other is the particle state. Much like time travelling back to time and saving the world, while your true self is busy sleeping.
Don’t take time travel part seriously, but the Quantum Theory is indeed True.
As impossible as it sounds, it is possible, and it can be used to improve processing speeds exponentially faster than supercomputers.
How much processing power is enough?
It can never be truly said. Processing power is the same as a person greed for money, the more you have it the greedier you become. Some assumptions about the need of processing power required in future were largely wrong.
Howard Hathaway Aiken, the original conceptual designer behind IBM’s Harvard Mark-I computer in 1940’s, stated that just 6 digital computers would satisfy the computing needs of the United States (What?).
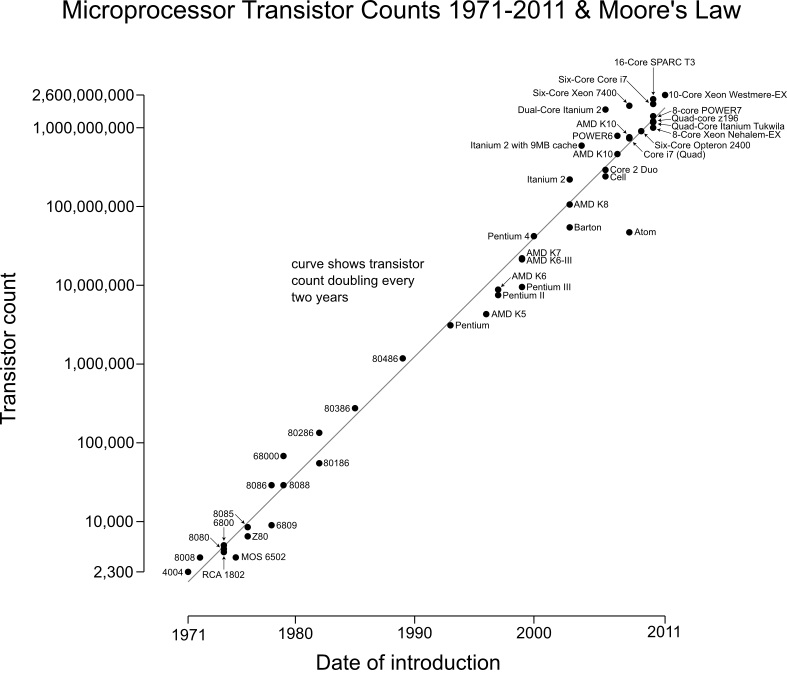
One Law that is almost true until now, is the Moore’s Law, which states that the number of transistors on a microprocessor continues to double every 18 months. As of 2016, the largest transistor count in a commercially available single-chip processor is over 7.2 billion—the Intel Broadwell-EP Xeon.
Talking in layman terms, the transistors comprises registers used to; Avoid instructions from having to leave the chip (i.e. go to RAM) to complete and keep the pipeline full or avoid going to RAM by predicting dependency outcomes.
Making Quantum Computers Possible!
The idea of Quantum computing was given by a physicist. Paul Benioff is credited with first applying quantum theory to computers in 1981.
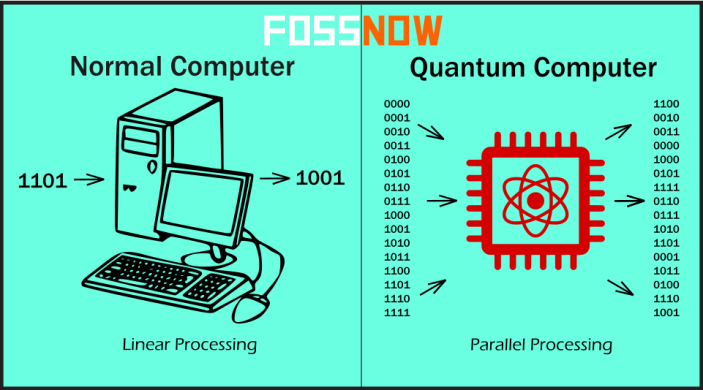
Quantum computers are different from binary digital electronic computers based on transistors. Whereas classical computers require that the data be encoded into binary digits (bits), each of which is always in one of two definite states (0 or 1).
Classical computers encode information as bits, that can be in one of two states, 0 or 1. Quantum computation uses quantum bits, or qubits, which can exist in ‘superposition’ of states that is, a single qubit can be either 0 or 1 or superposition of 0 and 1. Layman Terms: Qubits exist in a form of rotating sphere (electron spin), with spin either in direction of axis x, y or z which may be spinning down, orup or maybe right(superposition). We represent it here as 0, 1, superposition.

Consider a two-level quantum system, where a qubit, is in a two configuration system for each cell. Physicists like to call this a two-level system (TLS.)
The quantum state of a two level system one qubit is given by,
|ψ = α|0 + β|1 (Not exact formula)
A pair of qubits two qubits can be in any quantum superposition of 4 states,
|ψ = α00|00 + α01|01 + α10|10 + α11|11 (Not exact formula)
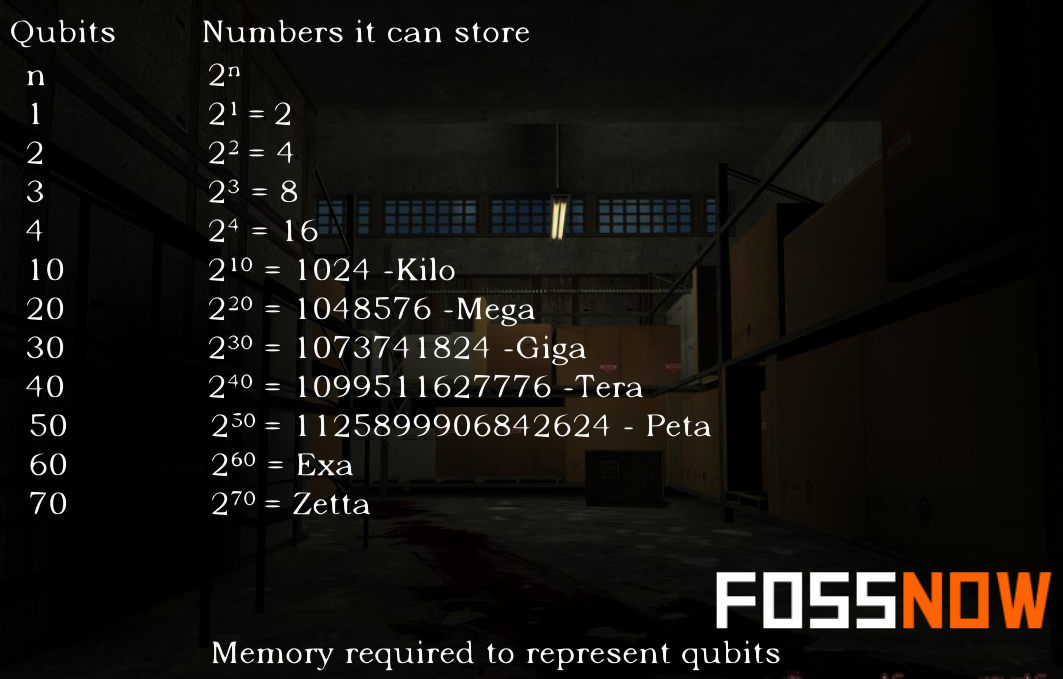
Three qubits in any superposition of 8 states. In general, a quantum computer with n qubits can be in an arbitrary superposition of up to 2n different states simultaneously (this compares to a normal computer that can only be in one of these 2n states at any one time)
This, together with qubits’ ability to share a quantum state (a state of a quantized system which is described by a set of quantum numbers as shown in above formula.) is called ‘entanglement’, which should enable the computers to essentially perform many calculations at once enabling parallel processing. And the number of such calculations should, in principle, double for each additional qubit, leading to an exponential speed-up.
Quantum Computers thus have the potential to perform faster than any silicon-based computer, as proved above.
Not as simple as it sounds.
A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits.
For example, representing the state of an n-qubit system on a classical computerrequires the storage of 2n complex coefficients, while to characterise the state of a classical n-bit system it is sufficient to provide the values of the n bits, that is, only n numbers.
Quantum algorithms are often probabilistic, in that they provide the correct solution only with a certainly known probability, not non-deterministic.
This is due to its superposition of up to 2n states. However, by repeatedly initializing, running and measuring the quantum computer’s results, the probability of getting the correct answer can be increased.
Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before the measurement.
It is generally incorrect to think of a system of qubits as being in one particular state before the measurement since the fact that they were in a superposition of states before the measurement was made directly affects the possible outcomes of the computation.
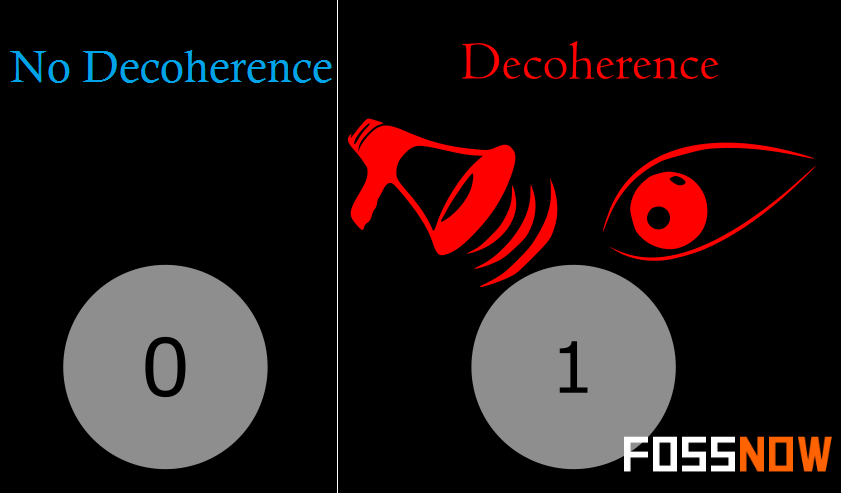
One of the greatest challenges is controlling or removing quantum decoherence.This usually means isolating the system from its environment as interactions with the external world cause the system to decohere.
Cypher or Cryptography breaking with Quantum Computer.
Integer factorization, which is an essential part of the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes). But qubits can make it possible.
By comparison, a quantum computer could efficiently solve this problem using Shor’s algorithm to find its factors, provided qubit doesn’t get affected by decoherence. This ability would allow a quantum computer to decrypt many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem.
By comparison, a quantum computer could efficiently solve this problem using Shor’s algorithm to find its factors, provided qubit doesn’t get affected by decoherence. This ability would allow a quantum computer to decrypt many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem.
In particular, most of the popular public key cyphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor’s algorithm specifically made for quantum computers. In particular, the RSA, Diffie-Hellman, and Elliptic curve Diffie-Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data.
It can even crack Digital Signatures, so they could sign with you on a document without either of the sender or the receiver knowing.
But, other cryptographic algorithms do not appear to be broken by those algorithms. More precisely the algorithms which do not primarily depend on factorization and discrete logarithm problems to which Shor’s algorithm applies, like the McEliece cryptosystem based on a problem in coding theory.
Conclusion:
Quantum computers may take over the technology world as well as help us in various fields of research like aviation, crypto analysis, medical, where a DNA in a single organism is 150 Zettabytes (1021) even storage of which is not possible in classical computers. Maybe Robots with Quantum Computers will take over the world, Who knows what will happen!!!
Source: FossNow By Danish Khan



Comments